E aí! Já treinou bastante os outros conteúdos do blog? Já sabe desenvolver fatoriais, permutações e arranjos, e agora está fera. Quer aprender mais ainda?

Então vamos aprender mais um conteúdo legal de análise combinatória.
Caso surgir alguma dúvida navegue pela aba

• Análise combinatória ►

Combinação simples.

Denominamos combinações simples de n elementos distintos tomados p a p aos subconjuntos formados por p elementos distintos escolhidos entre os n elementos dados.

É importante observar que duas combinações são diferentes quando possuem elementos distintos, não importando a ordem em que os elementos são colocados.

Representando por C_n,p o número total de combinações de n elementos tomados p a p , temos a seguinte fórmula:

“Combinação simples de n elementos tomados p a p ( 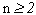) são subconjuntos com exatamente p elementos que se podem formar com os n elementos dados”.

Vamos relembrar alguns conceitos de arranjos.

Vamos passear um pouco por arranjos, e depois vamos seguir no mesmo exemplo trabalhando com combinação.

Vejamos um exemplo clássico.

1) Vamos considerar o conjunto A = {1,2,3,4,5}

Agora vamos formar todos os arranjos possíveis de 2 elementos distintos do conjunto A.

(1,2) (1,3) (1,4) (1,5) (2,3) (2,4) (2,5) (3,4) (3,5) (4,5)

(2,1) (3,1) (4,1) (5,1) (3,2) (4,2) (5,2) (4,3) (5,3) (5,4)

Porque (1,2) ≠ (2,1) ; (1,3) ≠ (3,1) , etc.

Note que usamos ( ) para denotar arranjos, pois são pares ordenados, o que implica em elementos distintos em cada agrupamento.

A simples mudança de ordem gera um novo par ordenado.

Então, utilizando a fórmula geral para arranjos simples. Onde

n= 5 (número total de elementos do conjunto A)

p= 2 (número de elementos tomados p a p – tomamos 2 elementos de cada vez para fazer os agrupamentos)

Observe que trabalhamos com 2 elementos tomados p a p, do conjunto com o total de n=5 elementos. Ou seja, fizemos arranjos de 2 a 2 com os 5 números do conjunto A.

Mas, e se quisermos saber, quantos subconjuntos de 2 elementos, podem ser formados por estes arranjos. Como proceder? Agora a conversa muda um pouco! Vamos ver como fica.

Os subconjuntos de 2 elementos que podemos formar são:

{1,2}, {1,3}, {1,4} ,{1,5} ,{2,3} ,{2,4} ,{2,5} ,{3,4}, {3,5}, {4,5}

Desta forma temos:
, porque {1,2}={2,1} ; {1,3} = {3,1} , etc.

Note que usamos {} para denotar combinações, pois são subconjuntos, e a ordem dos elementos num subconjunto não se altera.

E com 3 elementos como fica? O número de arranjos será:

Temos:

E o número de subconjuntos será:

Já deu para perceber que:

Vamos ver agora alguns exemplos mais elaborados.

Exercícios resolvidos de combinações simples.

1) Uma prova consta de 6 questões, das quais o aluno deve resolver 3. De quantas formas ele poderá escolher as 3 questões?

Quer-se agrupar 3 elementos, dentre os 6 existentes.

Perceba que a ordem em que os elementos aparecerão não será importante, uma vez que, ao resolver a 1ª , a 2ª e a 3ª questão é o mesmo que resolver a 2ª , a 3º e a 1ª, portanto é um problema de combinação.

Logo, um aluno pode escolher suas 3 questões de 20 maneiras diferentes.

Observe que, se quiséssemos apenas fazer os arranjos destes elementos 3 a 3, teríamos:

Faça você os arranjos, e depois verifique como foi feito nos exemplos anteriores, que esta afirmação é verdadeira.

2) De quantos modos distintos Amiroaldo pode escolher quatro entre as nove camisetas regata que possui para levar em uma viagem para Mosqueiro.

Suponha que Amiroaldo escolha as camisas 1, 2, 3 e 4.

Amiroaldo escolhendo as camisas:

Fonte camisa: http://www.portalimpacto.com.br/

Veja que (1, 2, 3, 4) = (1, 3, 4, 2), pois não importa em que ordem Amiroaldo escolhe as camisas que vai levar, o importante é que as camisas escolhidas são as mesmas na primeira e na segunda situação. Problemas como esses são resolvidos com a idéia de Combinação simples.

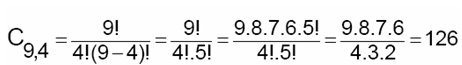
Existem 126 maneiras diferentes para Amiroaldo escolher 4 camisetas das 9 que possui.

Se fosse calculado o número de arranjos destas camisetas tomadas 4 a 4, teríamos 3024 arranjos.

Faça você os arranjos, e depois verifique como foi feito nos exemplos anteriores, que esta afirmação é verdadeira. (Brincadeira! Para você verificar a veracidade desta afirmação, vou dar uma dica de um software legal para você conferir as respostas dos exercícios propostos - Baixar software -:).

É só baixar e descompactar em uma pasta de sua preferência.
Observação:

- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.

- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

3) Ane, Elisa, Rosana, Felipe e Gustavo formam uma equipe. Dois deles precisam representar a equipe em uma apresentação. Quais e quantas são as possibilidades?

Representamos cada pessoa por uma letra

A: Ane;

E: Elisa;

R: Rosana;

F: Felipe;

G: Gustavo.

Precisamos determinar todos os subconjuntos de 2 elementos do conjunto de 5 elementos {A,E,R,F,G}. A ordem em que os elementos aparecem nos subconjuntos não importa, pois Ane-Elisa, por exemplo, é a mesma dupla que Elisa-Ane.

Então, os subconjuntos de 2 elementos são?

{A,E},{A,R},{A,F},{A,G},{E,R}{E,F},{E,G},{R,F},{R,G}{F,G}.

Chamamos estes subconjuntos de combinação simples de 5 elementos tomados com 2 a 2. Escrevemos C_5,2 .

Onde C_{5, 2} representa a fórmula das combinações simples:

Substituindo na fórmula

Preste atenção nesta próxima propriedade das combinações.

Propriedade importante das combinações:

De modo geral temos que:

C_{n, p} = C_{n, n-p}

Confirme esta propriedade utilizando o software Mathsys.
Observação: Siga os mesmos conselhos dados na observação anterior

Existem notações diferentes para combinações simples. Vamos usar uma em particular, pois será muito importante nos familiarizar-mos com ela.

Veja que:

Veja que, a frase “Vários caminhos levam a Roma” , se encaixa bem nesta parte do texto, pois.

Vamos ver alguns exemplos.

Exercícios resolvidos – Número binomial de ordem n e classe p.

1º - Vamos calcular o valor de:

5º - No jogo de truco, cada jogador recebe 3 cartas de um baralho de 40 cartas(são excluídas as cartas 8, 9 , 10).

De quantas maneiras diferentes um jogador pode receber suas 3 cartas

As 3 cartas diferem entre si pela natureza delas, e não pela ordem. Como a ordem não importa, calculamos?

Portanto, cada jogador pode receber suas 3 cartas de 9880 maneiras diferentes.

Faça estes exercícios com as outras notações. Lembre que, matemática só se aprende praticando muito.

Por enquanto é isso. Ficamos por aqui, mas em breve serão disponibilizados exercícios e mais alguns conceitos e curiosidades sobre este conteúdo.

• Análise combinatória ►

Se você deseja baixar o conteúdo deste artigo em formato PDF, baixe o arquivo:

MATEMÁTICA NA VEIA - ANÁLISE COMBINATÓRIA - COMBINAÇÕES SIMPLES

Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!

Se você quer cooperar com dicas, indicar algum blog legal de matemática, programas legais que conhece, artigos, trabalhos de escola. Fique a vontade. Mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo. Por enquanto ficamos por aqui! Agradeço antecipadamente, comentários, dicas, criticas e sugestões.

Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

VII) BIBLIOGRAFIA:

DANTE, Luiz Roberto. Matemática Dante Volume único, São Paulo, 1º edição, Ática, 2009.

DANTE,P.J. & HERSH, R. A experiência matemática, Rio de Janeiro, Francisco Alves, Ática, 1997.

BEZERRA, Manoel Filho. Matemática para o ensino médio, Volume único, Manoel Jairo Bezerra. São Paulo, Scipione (Série parâmetros). 2004, 5º Edição.
Matemática - vol 3, 2º grau aula 52. TIZZIOTTI,

Adaptações e imagem - camisa
http://www.portalimpacto.com.br/